字符串匹配

发表于 | 分类于

字符串匹配

在了解kmp算之前，先来看一下最简单的字符串匹配算法。

BF算法

这个算法，比较暴力，也比较容易理解，不做过多描述，下面给出一张图，一般都能理解。

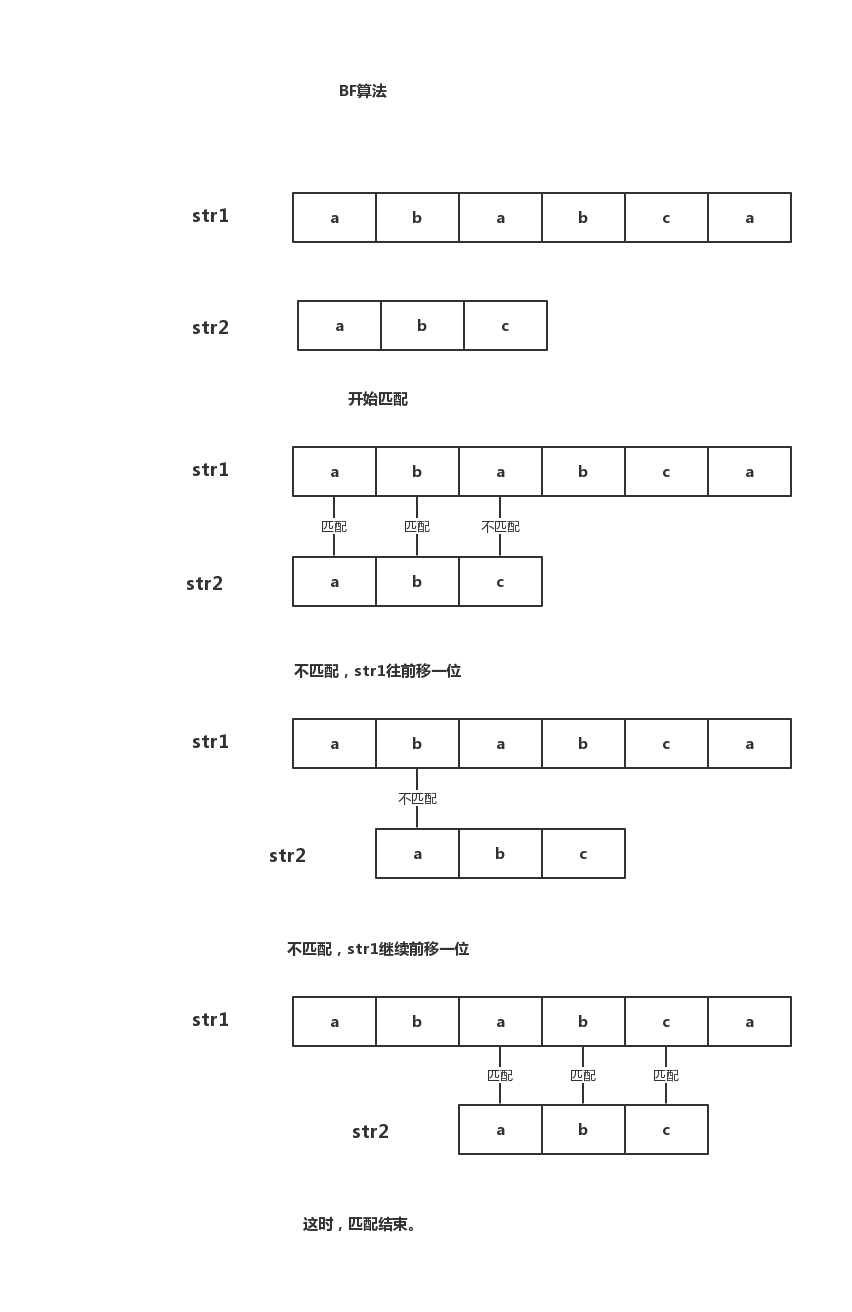
很简单，下面直接给出代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public class BF {
    public static void main(String[] args) {
        String str1 = "123123234";
        String str2 = "31";
        boolean result = bf(str1,str2);
        System.out.println("str1中是否包含str2:"+result);
    }
    public static boolean bf(String str1, String str2){
        int i = 0,j = 0,index = 0;
        while(i<str1.length()&&j<str2.length()){
            /**
             * 当str1[i]==str2[j]时，i,j同时加一
             * 当不相等时，j移动到0位置,i移动到index记录的下一位
             * 结合图片会更容易理解
             */
            if (str1.charAt(i)==str2.charAt(j)){
                i++;
                j++;
            }else {
                index++;
                i = index;
                j = 0;
            }
        }
        if (j == str2.length()){
            return true;
        }else {
            return false;
        }
    }
}

KMP算法

之所以先讲一个简单的方法，主要是让大家先了解一下这个算法是干嘛的，我认为kmp比较难的地方是他的next数组的计算方法，之前也写过一篇kmp相关的博客，但是自己回头看看讲的还是不够详细，这里再次完善一下。

很多书都是直接直接将的next数组的求解公式，直接给出来，但是即使理解了公式也不会写代码，很多都是靠死记硬背写出来的，所以我就想把这个过程详细的记录一下。

next数组

首先要明白，next数组它求的到底是个什么东西，下面简单举个例子。

a b a c a b a
0 1 2 3 4 5 6

比如我们要求解下标为3的位置上的next值，那我们需要求的就是：

a b a c a b a
0 1 2 3 4 5 6

下标为3的next值是通过计算它之前元素的最长公共前后缀得出的。

a b a
     

它的最长公共前后缀就是带颜色标记的，长度为1。（注：前缀和后缀不包含它本身）

下标为零的next值默认为-1。

下面在举一个比较通用的例子：

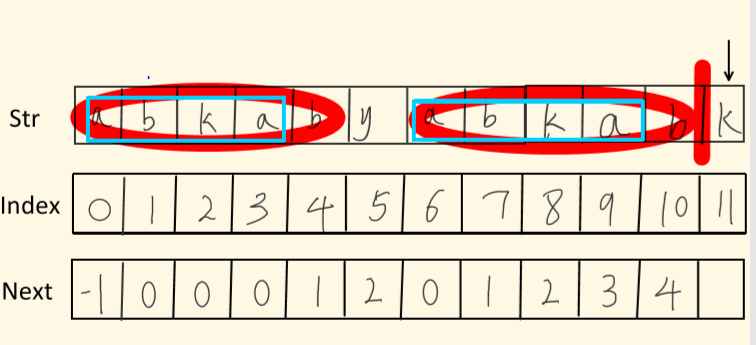
图1

前面的都已经求出来了，现在想要求下标11位置的next值，那我就可以根据10位置的next值求出来，蓝色框住的部分是已经求好的，而蓝色框后面的元素都是b所以，我可以在原有基础上加1，得出11位置的值为5。（注：求解最长公共前后缀的时候，前缀一定有第一个，后缀一定有最后一个）

为什么加一？

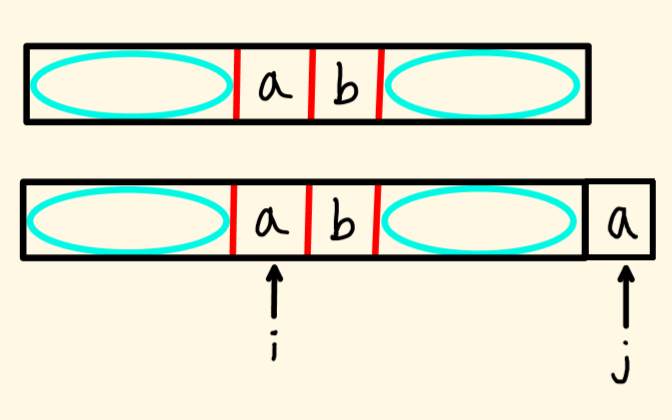
图2

这里蓝色块表示前一个位置的最长公共前后缀，而当我们多加了一个元素a的时候，在求最长公共前后缀的时候，就得比较新增j指向的元素和前缀的后一位，即i指向的元素，看他们两个是否相同，如果相同直接加一。

当然，不可能每次比较都会相同，现在我们来看一个不相同的例子。

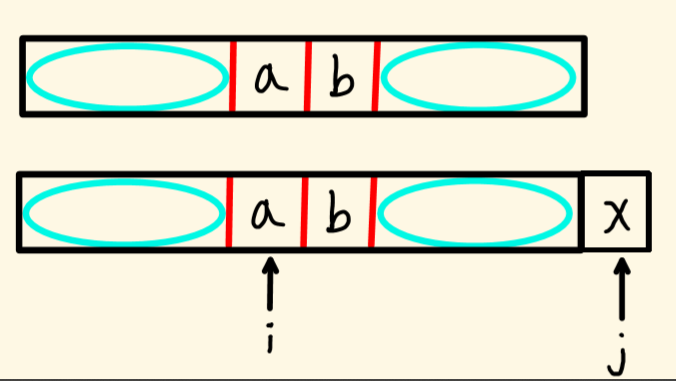
图3

这个时候i指向的元素和j指向的元素就不相同了，这是我们因该怎么做呢？

请看下面这幅图：

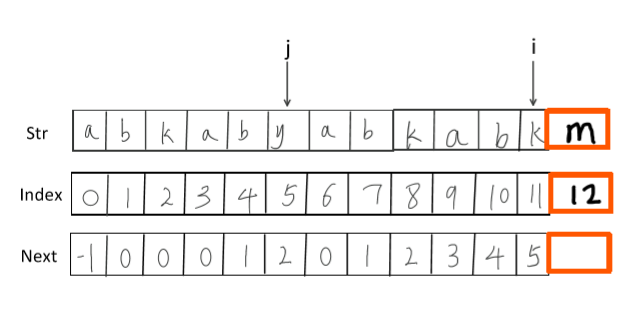
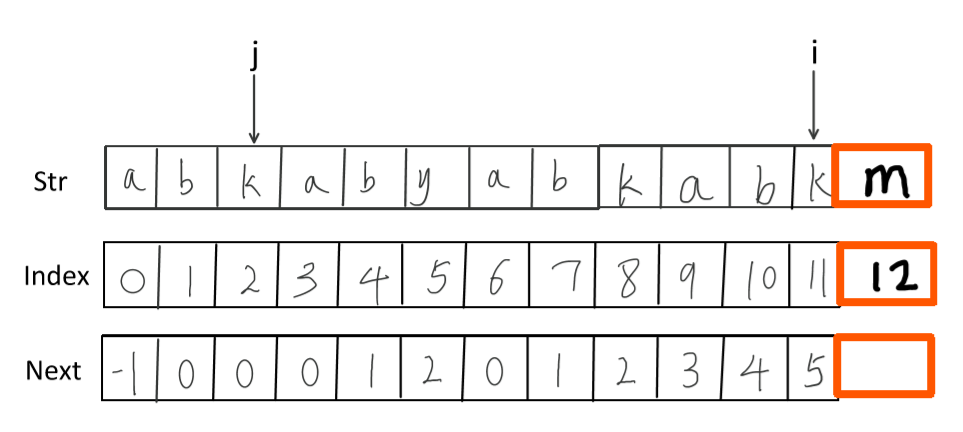
图4

这幅图中，我们需要求的是下标为12的index值，我们需要求的就是m之前的最长公共前后缀，下面我们来看如何基于已有的值推出下一个位置的index值。

我们看到i和j指向的元素不同，这时我们需要对j的指向进行调整，j位置的next值为2，将j的指向移动到下标为2的位置。

图5

这时，发现i和j能够匹配上了。下面在简单解释一下为什么会这样，后面的部分也会用到。

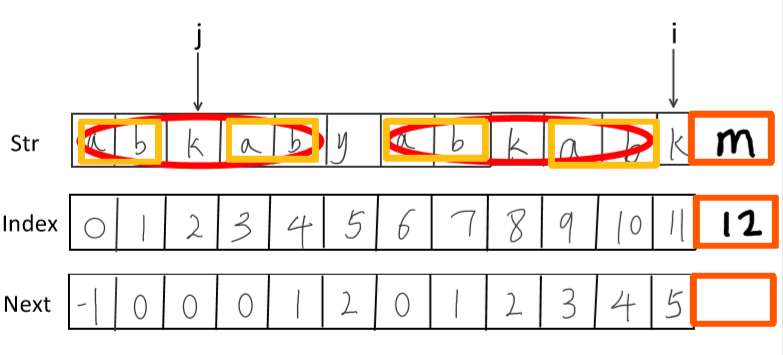
图6

我用几种不同颜色把公共的部分标注出来。

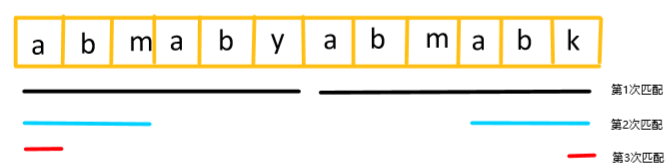
现在我把图4中已经匹配好的以及即将要匹配的部分拿出来，即abkaby和abkabk这两个字符串，我们这次匹配是在abkab这个最长公共前后缀的基础上求的，但是在这个基础上我们发现他们匹配不上，这是我们需要找一个第二长的公共前后缀，我们找到了ab，然后i和j就变成了图6现在的指向了。(注：我们求的是最长公共前后缀，所以必须包含前缀的第一位和后缀的最后一位，剩下的就自己思考吧)。

这时，我们就可以把思路整理一下，然后开始撸代码了。

求next串的代码

上面有一种特殊情况没考虑，这里说明一下。

在第三次匹配的时候，它也没匹配到(第一位的next值为-1)，所以下一次匹配他会匹配到找下标为-1的值，但是很显然-1这种情况就是没有公共前后缀，所以给他赋值为0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public static void getNext(char[] pattern,int[] next){
    //为i和j赋初始值
    int i = 0,j = -1;
    //首先为第一位赋值为-1,
    next[0] = -1;
    //获取模式串的长度
    int len = pattern.length;
    while(j == -1|| i < len){
        /**
         * 这里如果j是-1，++j就是零，
         * 或者他们相等的话就将next值在原有的基础上加一
         * 那我们就可以将这两种情况统一成下面这种形式，
         * 否则就让他匹配第二长的最长公共前后缀
         */
        if (j == -1||pattern[i] == pattern[j]){
            next[++i] = ++j;
        }else {
            j = next[j];
        }
    }
}

主串和模式串的匹配代码

匹配过程，如下所示。

例子：

j 0 1 2 3
模式串 a a a b
next[j] -1 0 1 2

首先从头开始匹配，直到找到一个不匹配的字符。

j下标指向     i          
  0 1 2 3 4 5 6 7
主串 a a b a a a a b
模式串 a a a b        
j下标指向     j          

这时我们需要将将模式串往前回溯，但是回溯到哪里呢？这时就用到了我们的next数组。

j指向的位置的next的值表示它之前的最长公共前后缀，并且这里是到j位置才不能匹配上的，所以之前的都是相同的，那我们就可以把模式串的前缀匹配到主串的后缀(注：这里所说的前后缀表示的是已经匹配上的字符串)，变成下面这种情况。

j下标指向     i          
  0 1 2 3 4 5 6 7
主串 a a b a a a a b
模式串   a a a b      
j下标指向     j          

可以看出，j之前的元素都已经匹配上了，这就是前后缀next值帮我们做到的，这样我们就不用像BF算法一样每次都从头开始匹配了，但是i和j指向的元素仍然没有匹配上，我们需要继续往前回溯，变成下面这样。

j下标指向     i          
  0 1 2 3 4 5 6 7
主串 a a b a a a a b
模式串     a a a b    
j下标指向     j          

这时依然没有匹配上，但是模式串已经到末尾了，所以将i往前移动一位。

j下标指向       i        
  0 1 2 3 4 5 6 7
主串 a a b a a a a b
模式串       a a a b  
j下标指向       j        

下面就同理了，不在赘述了，最终结果：

j下标指向               i
  0 1 2 3 4 5 6 7
主串 a a b a a a a b
模式串         a a a b
j下标指向               j 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public static void kmp(char[] s,char[] pattern,int[] next){
    int j = 0,i = 0;
    //主串长度
    int len1 = s.length;
    //模式串长度
    int len2 = pattern.length;
    //begin和end表示模式串在主串的开始和结束位置
    int begin = 0,end = 0;
    while (i < len1){
        /**
          *当j=-1时，说明模式串已经回溯到头了
          *将i+1，j+1,i相当于往前移动了一位，j从0开始匹配
          *当s[i] == pattern[j]，i和j同时加1,
          *否则，就往前回溯
          */
        if (j == -1||s[i] == pattern[j]){
            i++;
            j++;
        } else {
            j = next[j];
            begin = i - j;
        }
        //判断模式串是否所有元素都已经匹配上了，匹配上的话，直接退出while循环
        if(j == len2){
            end = i;
            break;
        }
    }
    //输出结果
    if (j == len2){
        System.out.println("模式串在主串的下标为从"+begin+"到"+end);
    }else {
        System.out.println("没有匹配的字符串");
    }
}