最长公共子序列

发表于 | 分类于

什么是子序列

在数学中，某个序列的子序列是从最初序列通过去除某些元素但不破坏余下元素的相对位置（在前或在后）而形成的新序列。详情请查看wike百科。 举个例子：[a,b,c,d,e]，如果找一个子序列，可以是[a,b,c],[a,c,e],[b,e],但不可以是[c,a,e],这个例子举得比较特殊，下标越大，字母越靠后，而如果原本下标比较小得字母排到下标大的后面，这就不符合子序列的定义了。

什么是最长公共子序列

这个不需要多说，如果是求数组A和B的最长公共子序列，就是说既是A的子序列又是B的子序列，而且要保证最长。

推理

设$L(m,n)$表示$X=[x_1,x_2,…,x_m]$和$Y=[y_1,y_2,…,y_n]$的最长公共子序列的长度。

推导的函数如下：

  • 解释 当$x_i=y_j$时，$L(i,j)=L(i-1,j-1)+1$

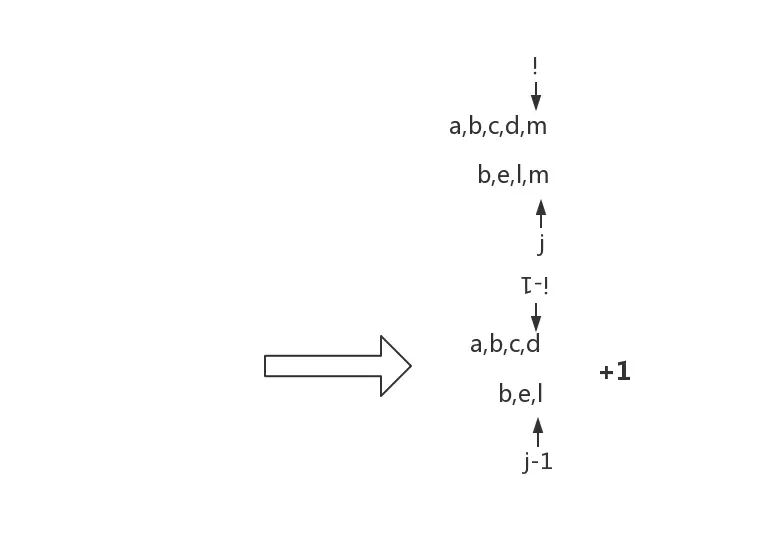
SubString1.jpg

根据这个例子，当i和j指向的元素相同时，这时求$L(i,j)$的最大值就是$L(i-1,j-1)+1$。

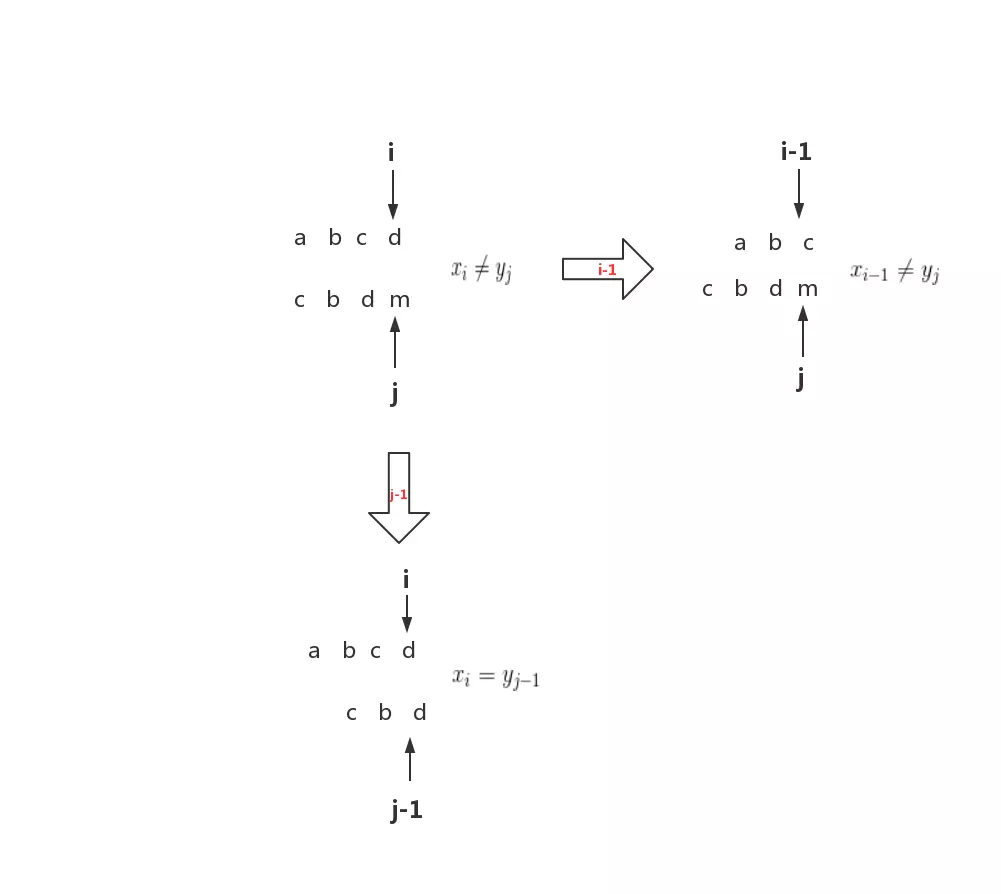
当$x_i \neq y_j$时，$max\begin{Bmatrix} L(i,j-1),L(i-1,j) \end{Bmatrix}$ SubString2.jpg

当取i-1和j-1时，可能会使$x_i=y_{j-1}$或$x_{i-1}=y_j$,当然也可能两种情况都不相等，本着最长得原则，所以从$L(i,j-1)$和$L(i-1,j)$中找一个最大值，然后重复此过程。

递归函数：

1
2
3
4
5
6
7
8
9
10
    public int MaxSubsequence(String a, String b, int i, int j){
        if (i<0||j<0){
            return 0;
        }
        if (a.charAt(i)==b.charAt(j)){
            return MaxSubsequence(a,b,i-1,j-1)+1;
        }else {
            return Math.max(MaxSubsequence(a, b, i - 1, j), MaxSubsequence(a, b, i, j - 1));
        }
    }

这个想法很容易写，但是速度相对较慢，当提交到leetcode上(注：leetcode1143题)时，会超时，所以要想一种新得做法。

动态规划

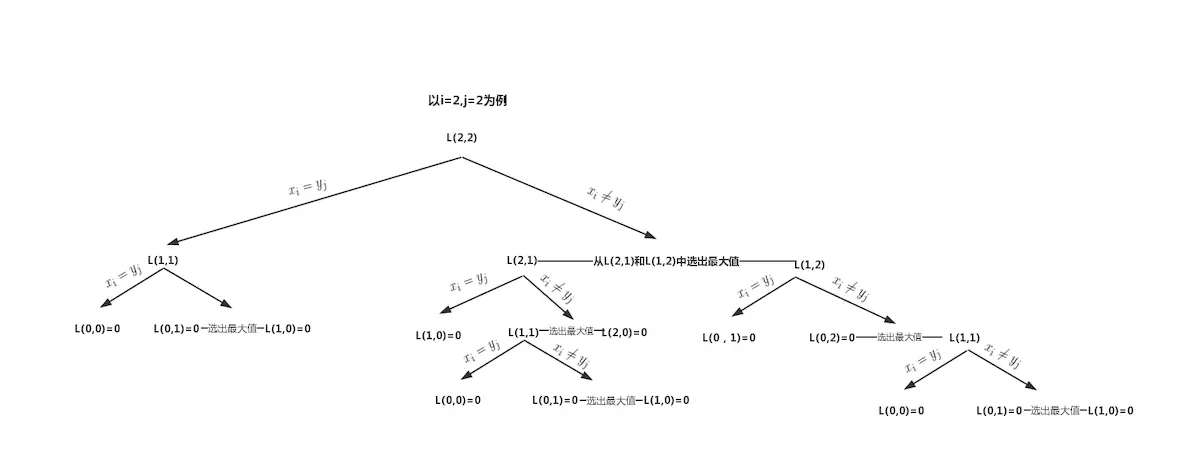
先看一个例子： SubString3.jpg

这个图看着可能稍微有一点乱，但是大致意思也能表示出来，这是上面递归方法做出的结果，可以看出这里会重复计算$L(1,1)$,当$i，j$的值越大，重复计算的数就越多，所以递归的方法速度就会相对较慢，为了解决这个问题，我们可以把计算结果存储起来，下次使用时直接拿就行了，进而加快速度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
  public static int dp(String text1, String text2){
        int m = text1.length();
        int n = text2.length();
        int[][] arr = new int[m+1][n+1];
        /**
         * 根据推导公式，如果X_i==Y_j，arr[i][j]=arr[i-1][j-1],
         * 否则arr[i][j]=Max{arr[i-1][j],arr[i][j-1]}
         */
        for(int i=1; i<=m; i++){
            for (int j=1;j<=n; j++){
                if (text1.charAt(i-1)==text2.charAt(j-1)){
                    arr[i][j]=arr[i-1][j-1]+1;
                } else{
                    arr[i][j]=Math.max(arr[i-1][j],arr[i][j-1]);
                }
            }
        }
        return arr[m][n];
    }

上面代码需要注意的是，使用的是text1.charAt(i-1)==text2.charAt(j-1)，因为iString下标从零开始，如果我们使用text1.charAt(i)==text2.charAt(j)，那么两个字符串的第一个将被我们忽略（因为我在写的时候结果会比真正结果小一）。