堆排序

发表于 | 分类于

什么是堆？

堆通常是一个可以被看做一棵完全二叉树的数组对象。——百度词条

堆又分为大根堆和小根堆

  • 大根堆（最大堆），即每个父节点都大于等于他的子节点
  • 小根堆（最小堆），即每个父节点都小于等于他的子节点 一般情况下，堆排序使用的是最大堆。

做堆排序之前的准备工作

如何将一个数组变成为一个最大堆

首先将数组和二叉树对应起来

先看一个例子： [4 8 3 6 1 2]这个数组是下面这棵完全二叉树通过从上到下、从左到右的顺序遍历的结果，这样我们就可以看出数组的下标和完全二叉树之间的关系了。 堆.PNG 这里的i表示第i个节点，parent(i)表示第i个节点的父节点，left(i)表示第i个节点的左孩子，right(i)表示第i个节点的右孩子。
以8为例，8的下标是1，即i=1,它的父节点为$(1-1)/2=0$，左孩子就是$1 \times 2 + 1 = 3$，右孩子为$1\times2+2=4$。确定好数组和二叉树的对应关系，接下来就是如何将二叉树变成一个最大堆。

生成最大堆

生成最大堆我们就需要将节点的值进行交换，但是交换的时候就要考虑是从下到上，还是从上到下交换，我一般喜欢从下往上，因为我没感觉比较符合一般递归的思路，就以下面这个为例： image.png 从下往上我们应该从下面那个元素开始呢，我们一般都是从最后一个叶子节点的父节点开始的，因为最后一个叶子节点就是数组的最后一个元素，即这里的2，所以使用起来比较方便，又根据上面求父节点的公式可知，第一个进行比较的节点是下标为3的元素。这里下标为3的元素的值比其左右孩子的值大，所以不用交换。
那下一个进行比较的节点是哪个呢，因为叶子节点是没有左右孩子的，所以不考虑叶子节点，之后我们选择下标为2的节点进行比较（这里为什么选择2，下面会进行说明），下标为2的元素比其左右孩子都大，不用交换。
然后对下标为1的节点做同样操作，最后对根节点做比较。 下面说明一下上面选择下标为2进行比较的原因： image.png 根据这张图可以看出，我们进行比较的顺序，既是从下往上，而且还具有规律，即进行比较的元素下标从第一个开始的下标逐渐减小到零，这样为我们编写代码提供了便利。
其实，这里还有一个问题，上面为了简化过程就直接拿一个已经是最大堆了，下面举个反例： image.png 从图上可以看出，1的左子树已经是最大堆了，右子树也是，但是按照原来的规则修改之后，变成： image.png 右子树不满足最大堆的定义了，这里我们还用进行一步比较，变成： image.png 请大家记住这种情况，这里是我们之后写代码为什么需要递归的原因。

开始编写建最大堆的代码（java代码）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
    public void swap(int[] arr,int a,int b){
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }
//heapify函数的作用是父节点与左右孩子节点进行比较，判断父节点是否   
//大于左右孩子，不大于则进行交换，这里进行递归是防止出现上面讲到的那种情况
    public void heapify(int[] tree,int n,int i){
        if (2*i+1>=n){
            return;
        }
        int c1 = 2 * i + 1;
        int c2 = 2 * i + 2;
        int max = i;
        if (c1 < n && tree[c1] > tree[max]){
            max = c1;
        }
        if (c2 < n && tree[c2] > tree[max]){
            max = c2;
        }
        if (max != i){
            swap(tree,max,i);
            heapify(tree,n,max);
        }
    }
//buildHeap函数是将二叉树从下往上进行比较，生成最大堆，即上面带有红色箭头部分的分析过程
    public void buildHeap(int[] tree, int n){
        int parent = (n-1)/2;
        for (int i = parent; i >= 0; i--){
            heapify(tree,n,i);
        }
    }

正式开始排序

我们继续举例： image.png 这已经是最大堆了，根据最大堆的定义或者看上面这张图，我们可以知道，最大值一定是根节点那个元素。 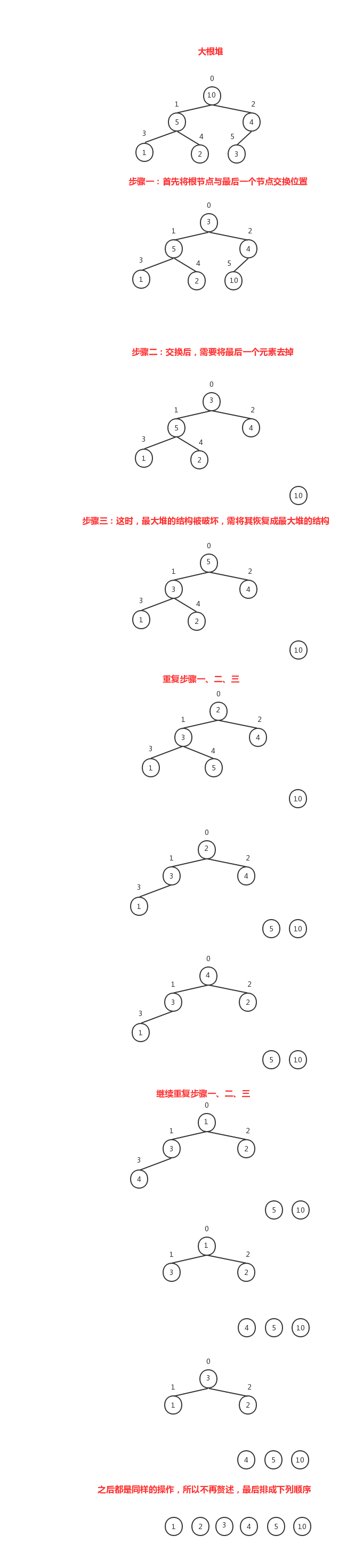heap.jpg 关于上图再进行一些说明，为了便于理解，上面说将最后一个元素去掉，这里其实不是去掉，因为这里我们一直操作的使数组，最后一个元素其实是放到了数组的末尾，我们不再对末尾的元素进行操作了，所以这里说成去掉了。就拿步骤六的结果来说，二叉树从上到下，从左到右便利的结果是：[3 1 2]，排好需的是[4 5 10]，这里排好后的结果并不是 去掉了而是放到了数组的末尾，合起来就是[3 1 2 4 5 10]。

排序代码实现

1
2
3
4
5
6
7
8
9
10
11
    public static void heapSort(int[] tree,int n){
        buildHeap(tree,n);
        //for循环相当于将最后一个节点取出操作，这里说取出不太恰当，这里其实是最后一个元素不再参与之后的操作了
        // 这里i不断减小，就是使排好顺序的元素不再进行操作了
        for (int i = n-1; i >= 0; i--) {
            //根节点和最后一个节点交换位置
            swap(tree,i,0);
            //交换后，我们需要将除最后一个节点外的节点继续按最大堆排列，这一步是恢复操作
            heapify(tree,i,0);
        }
    }

不足之处，还请指出，创作不易，转载请注明出处