HashMap源码学习

发表于 | 分类于

纸上得来终觉浅，觉知此事要躬行。 每次读书或者阅读文章都感觉“哦哦，原来是这样”，以为自己懂了，其实只是把别人的东西记到脑子里，遗忘的很快。好记性不如烂笔头，写写总归没有坏处。

好，正式开始，先上源码，比较长就直接给链接了。openjdk11的HashMap源码链接

当然，这里只会挑比较重要的部分进行记录，比如hash()，put()，get()等常用函数。

hash()函数

首先看一下hash()函数：

1
2
3
4
    static final int hash(Object key) {
        int h;
        return key == null ? 0 : (h = key.hashCode()) ^ h >>> 16;
    }

看到这个公式有点蒙，先看»>是个什么意思。这个符号与»的差别就是：

»>是不分正负的，右移统统在高位补零。在研究这个问题时发现，int型在进行移位运算时（»/»>/«）范围在0~31之间，超出后按零处理。（知识补充）

这里是将传入的对象的hash值的高16位与低16进行运算，为什么要这样呢？ 因为这里还有一步没在hash函数里显示所以不太能看懂，我们来看下面这段代码。

1
(n - 1) & hash （这段代码，在getNode和putVal函数中）

这虽然不在hash函数里，但是也起着重要的作用，这段计算公式可能不太好理解，换成下面这样可能就好理解多了：

1
hash % n（对我们的hash值进行取余操作，而n就是我们的数组大小）

之所以，高16为与低16位进行异或，是因为防止高位的变化对整个hash函数没有影响，这就好比10的倍数对10取余，无论倍数怎么改变，最终取余都为0，而高16为与低16位进行异或以后，高位的变化就会反映出来，有效的避免了这种情况，从而减少了hash冲突，HashMap的hash函数设计的还是比较巧妙的。

其实，对于(n - 1) & hash 还有另一种解释，只不过这种解释比较难理解。

n为2的整数次幂，也就是像4,8,16,32…这样的数，这样的数有一种规律，就是减一以后二进制低位变成全一。 假设我们的数组长度为5(0101),现在有待插入的数据1,2,3,4,5,6。（hash & (n - 1)）

0001(1) & 0100(4) = 0

0010(2) & 0100(4) = 0

0011(3) & 0100(4) = 0

0100(4) & 0100(4) = 4

0101(5) & 0100(4) = 4

0110(6) & 0100(4) = 4

可以看出，不管其他位置怎么变化与操作的结果只和4的二进制1的位置有关，这样的话，hash冲突就比较严重了，并且十分浪费空间。

当数组长度为2的整数次幂时：

假设长度为4(0100)，待插入数据1,2,3,4,5,6。

0001(1) & 0011(3) = 1

0010(2) & 0011(3) = 2

0011(3) & 0011(3) = 3

0100(4) & 0011(3) = 0

0101(5) & 0011(3) = 1

0110(6) & 0011(3) = 2

这时就能很好的减少hash冲突，其实这里还是和取余的意思相同，位操作相比于%速度更快一些。

但是这两段代码想要转换，必须满足一个条件：n是$2^k$，这也是为什么我们在声明map的大小时需要是2的整数次幂了。

1
2
3
4
    static final int tableSizeFor(int cap) {
        int n = -1 >>> Integer.numberOfLeadingZeros(cap - 1);
        return n < 0 ? 1 : (n >= 1073741824 ? 1073741824 : n + 1);
    }

这段代码保证了即使我们传入的值不是2的指数倍，它也会自动给我们转换化成最接近且不小于我们指定大小的2的指数倍。（对与HashMap将数组大小定义为2的整数次幂，其实还有一个作用，在resize()中介绍）

综上所述，hash函数应该为：

1
((h = key.hashCode()) ^ h >>> 16) & (n - 1)

put函数

在看put源码之前，我们先来看一下我们的值在map中是如何存储的。

看下面这张图（注：这里并不是map实际的插入过程，只是简单的将插入的数据对4取余得到的结果）：

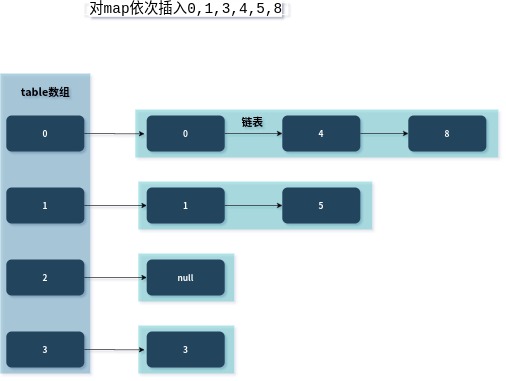
image1

虽然看起来效果还不错，但是这里却有个问题。

即使hash函数能够大大降低冲突，但是也不能完全避免，当出现下面这种情况时，map的查找速度就会大大降低：

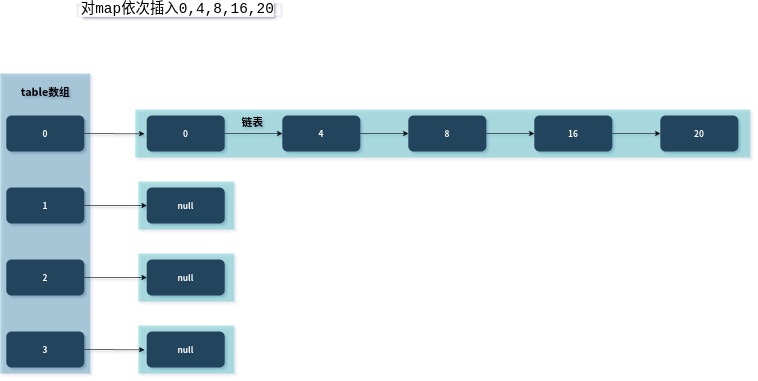
可以看到所有元素都集中到一条链表上了，这样的话，我们查询元素的时候，就需要遍历链表了，它的时间复杂度就会从O(1)下降到O(n)，即使这个概率很小。当然，java已经为我们解决了这个问题，来看看他是怎么解决的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
    public V put(K key, V value) {
        //真正的逻辑在putVal里
        return this.putVal(hash(key), key, value, false, true);
    }

    final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
        HashMap.Node[] tab;
        int n;
        //如果表空说明未初始化，所以先调用resize()先初始化。
        if ((tab = this.table) == null || (n = tab.length) == 0) {
            n = (tab = this.resize()).length;
        }

        Object p;
        int i;
        //查看待插入的位置是否为null，为null直接插入
        if ((p = tab[i = n - 1 & hash]) == null) {
            tab[i] = this.newNode(hash, key, value, (HashMap.Node)null);
        } else {
            Object e;
            Object k;
            //如过hash值相同且key相同，新传入的值就会把旧值给替换掉
            if (((HashMap.Node)p).hash == hash && ((k = ((HashMap.Node)p).key) == key || key != null && key.equals(k))) {
                e = p;
            } else if (p instanceof HashMap.TreeNode) {
                //如果p是TreeNode类型，说明已经树化了，那就按照红黑树的规则进行添加节点
                e = ((HashMap.TreeNode)p).putTreeVal(this, tab, hash, key, value);
            } else {
  				//判断该bin（待插入的链表）内有多少个元素，如果binCount>=7就进行树化（红黑树）
                int binCount = 0;
                while(true) {
                    if ((e = ((HashMap.Node)p).next) == null) {
                        ((HashMap.Node)p).next = this.newNode(hash, key, value, (HashMap.Node)null);
                        if (binCount >= 7) {
                            //树化
                            this.treeifyBin(tab, hash);
                        }
                        break;
                    }
					//这里和上面的逻辑一样,如果带插入的hash值与key与已经存入的相同，就更新值
                    if (((HashMap.Node)e).hash == hash && ((k = ((HashMap.Node)e).key) == key || key != null && key.equals(k))) {
                        break;
                    }

                    p = e;
                    //计算该bin内有多少个元素
                    ++binCount;
                }
            }
			//为找到的e节点赋值（更新的情况）
            if (e != null) {
                V oldValue = ((HashMap.Node)e).value;
                if (!onlyIfAbsent || oldValue == null) {
                    ((HashMap.Node)e).value = value;
                }

                this.afterNodeAccess((HashMap.Node)e);
                return oldValue;
            }
        }

        ++this.modCount;
        //如果size大于阀值，进行扩容
        if (++this.size > this.threshold) {
            this.resize();
        }
        this.afterNodeInsertion(evict);
        return null;
    }

对于put()函数在总结一点，这里当表内的一个bucket（有的叫桶，先理解表中一个链表）长度大于等于7（也就是第八个）时会进行树化，防止查询效率较低，这里树采用的是红黑树（一种比较稳定的数据结构查询、插入以及删除时间复杂度都是log(n)）。当删除到小于7的时候会再次转化为链表结构，因为维持红黑树是比较耗时的，数据量小就没必要使用红黑树了。使用红黑树的效果大致如下：

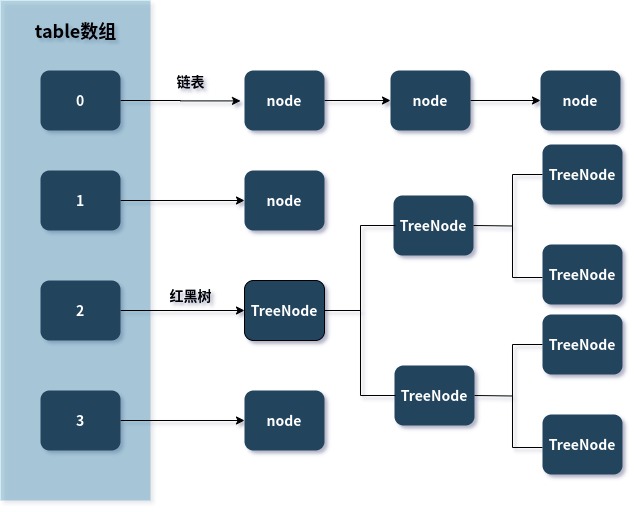
get()函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
    public V get(Object key) {
        HashMap.Node e;
        //调用getNode()函数
        return (e = this.getNode(hash(key), key)) == null ? null : e.value;
    }

    final HashMap.Node<K, V> getNode(int hash, Object key) {
        HashMap.Node[] tab;
        HashMap.Node first;
        int n;
       // 判断tab不为空或者经过取余以后映射到的位置不为空
        if ((tab = this.table) != null && (n = tab.length) > 0 && (first = tab[n - 1 & hash]) != null) {
            Object k;
            //如果头节点就是待查节点，直接返回
            if (first.hash == hash && ((k = first.key) == key || key != null && key.equals(k))) {
                return first;
            }

            HashMap.Node e;
            if ((e = first.next) != null) {
                //如果该节点是TreeNode类型的，调用getTreeNode函数查找
                if (first instanceof HashMap.TreeNode) {
                    return ((HashMap.TreeNode)first).getTreeNode(hash, key);
                }
				//否则，直接遍历查找链表
                do {
                    if (e.hash == hash && ((k = e.key) == key || key != null && key.equals(k))) {
                        return e;
                    }
                } while((e = e.next) != null);
            }
        }

        return null;
    }

get函数比较简单，没有太多要总结的。

resize()函数

这个函数主要有两个功能。

  • 1.初始化table数组
  • 2.对table数组进行扩容

下面直接看源码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
    final HashMap.Node<K, V>[] resize() {
        //第一次调用resize函数是在put函数中，当我们添加元素时，table数组还未初始化，table == null
        HashMap.Node<K, V>[] oldTab = this.table;
        int oldCap = oldTab == null ? 0 : oldTab.length;
        int oldThr = this.threshold;
        int newThr = 0;
        int newCap;
        if (oldCap > 0) {
            //如果table数组容量大于最大存储容量，则将阀值赋值为Integer.MAX_VALUE,直接返回该数组，不再进行扩容
            if (oldCap >= 1073741824) {
                this.threshold = 2147483647;
                return oldTab;
            }
			//如果table数组扩容一倍后不大于最大存储容量，则进行扩容，阀值也扩大一倍
            if ((newCap = oldCap << 1) < 1073741824 && oldCap >= 16) {
                newThr = oldThr << 1;
            }
        } else if (oldThr > 0) {
            newCap = oldThr;
        } else {
            //当table为null的时候就初始化一个默认大小的table数组
            newCap = 16;
            newThr = 12;//newCap * 0.75 = 12
        }
		//newThr == 0 为其赋值
        if (newThr == 0) {
            float ft = (float)newCap * this.loadFactor;
            newThr = newCap < 1073741824 && ft < 1.07374182E9F ? (int)ft : 2147483647;
        }
		//创建初始化或者扩容的数组
        this.threshold = newThr;
        HashMap.Node<K, V>[] newTab = new HashMap.Node[newCap];
        this.table = newTab;
        //如果是扩容，则需要将旧数组中的值依次拷贝进新数组
        if (oldTab != null) {
            for(int j = 0; j < oldCap; ++j) {
                HashMap.Node e;
                //为e赋值并判断是否为空
                if ((e = oldTab[j]) != null) {
                    //oldTab[j]指向null，以便java进行垃圾回收
                    oldTab[j] = null;
                    //如果e只有一个节点，直接赋值到新的bin中
                    if (e.next == null) {
                        newTab[e.hash & newCap - 1] = e;
                        //如果e是TreeNode类型，按照红黑树的规则转换
                    } else if (e instanceof HashMap.TreeNode) {
                        ((HashMap.TreeNode)e).split(this, newTab, j, oldCap);
                    } else {//否则拷贝进链表
                        HashMap.Node<K, V> loHead = null;
                        HashMap.Node<K, V> loTail = null;
                        HashMap.Node<K, V> hiHead = null;
                        HashMap.Node hiTail = null;

                        HashMap.Node next;
                        do {
                            next = e.next;
                            if ((e.hash & oldCap) == 0) {
                                if (loTail == null) {
                                    loHead = e;
                                } else {
                                    loTail.next = e;
                                }

                                loTail = e;
                            } else {
                                if (hiTail == null) {
                                    hiHead = e;
                                } else {
                                    hiTail.next = e;
                                }

                                hiTail = e;
                            }

                            e = next;
                        } while(next != null);

                        if (loTail != null) {
                            loTail.next = null;
                            newTab[j] = loHead;
                        }

                        if (hiTail != null) {
                            hiTail.next = null;
                            newTab[j + oldCap] = hiHead;
                        }
                    }
                }
            }
        }

        return newTab;
    }

这里再讲一下，2的整数次幂对扩容的作用

因为这里对数组扩容也是两倍两倍的增加，最终数组的长度也是一个2的整数次幂。

比如说原本数组长度为4，扩容以后为8，那这里就涉及到重新计算hash值了，以2,3,4,5,6,7为例。

0010(2) & 0011(3) = 0010(2) 0010(2) & 0111(7) = 0010(2)

0011(3) & 0011(3) = 0011(3) 0001(3) & 0111(7) = 0011(3)

0100(4) & 0011(3) = 0000(0) 0100(4) & 0111(7) = 0100(4)

0101(5) & 0011(3) = 0001(1) 0101(5) & 0111(7) = 0101(5)

0110(6) & 0011(3) = 010(2) 0110(6) & 0111(7) = 0110(6)

0111(6) & 0011(3) = 0011(3) 0111(7) & 0111(7) = 0111(7)

可以看出规律，小于为扩容前数组的大小的是不会发生变化的，而大于原先数组的都在扩容后数组长度减一后二进制最高位上加了个一。这样的话是否移动以及移动到哪就可以通过新hash值与原数组长度按位与，如果是0就不动，如果是1就移动到原索引加上扩容前数组长度。以3,5为例：

根据上面结果可知，3(0011) & 4(0100) = 0 不动，5(0101) & 4(0100) = 1(移动到1(原索引位置)+4 = 5)

具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//(e.hash & oldCap) == 0说明rehash的值小于原数组长度，仍在原来下标位置
    if ((e.hash & oldCap) == 0) {
        if (loTail == null) {
            loHead = e;
        } else {
            loTail.next = e;
        }
        loTail = e;
        //否则进入原下标加数组长度
    } else {
        if (hiTail == null) {
            hiHead = e;
        } else {
            hiTail.next = e;
        }

        hiTail = e;
    }



		//放入原下标
    if (loTail != null) {
        loTail.next = null;
        newTab[j] = loHead;
    }
			//放入原下标加原数组长度
    if (hiTail != null) {
        hiTail.next = null;
        newTab[j + oldCap] = hiHead;
    }

总体来说，put，get，resize这三个方法深层次去挖掘的话，还是比较难的，其中也涉及到比较难的数据结构（红黑树），这对理解HashMap的源码产生了一些影响。但是抛去细节来说，只要慢慢阅读，还是能够清楚的代码的答题思路的。